Everything about Random Forests

Random Forests are an increasingly popular machine learning algorithim. They perform well in a wide variety of learning and prediction problems despite being exceedingly easy to implement. Random forests can be used for both classification and regression problems.

This post describes the intuition of how Random Forests work as well as its. advantages and disadvantages.

Intuition for How Random Forests Work

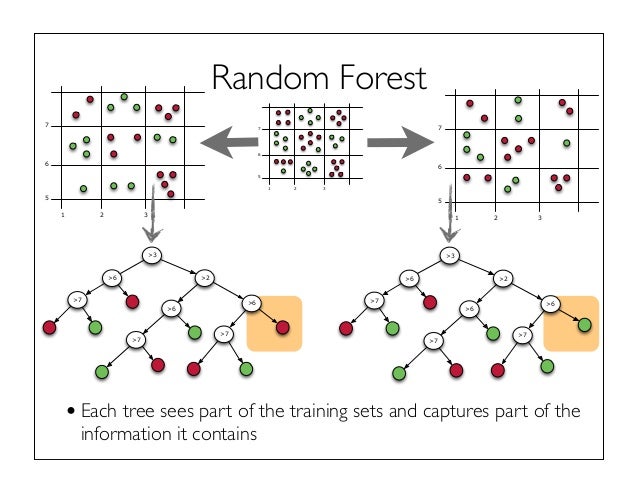
At a high level, the algorithim usually works as follows:

1. Randomly sample $N$ observations from the training set at random with replacement ¹
2. Train a decision tree using $N$ and $\sqrt{num\_features}$.

Repeat (1) and (2) B times, where B is the number of trees (also called bags). Depending on the nature of data, the ideal number of trees ranging from 100 to several thousand.

Source: Jan Vitek, Perdue

Main Advantages

Embarrassingly Parallel

SKlearn will allow you to use all the cores in your computer to train multiple trees at the same time. The algorithim is also available in Spark. This is because all random forests are trained independently of eachother.

Resistant to Overfitting

The only way to overfit the model is to have trees that have too many branches. Increasing the number of trees does not increase the risk of overfitting. Instead an increasing number of trees tends to decrease the amount of overfitting

No Need for Cross Validation

We can also avoid cross-validation by using the out of bag score. This is available as an argument in Spark and Sklearn and provides nearly identical results to N-fold cross-validation.²

Other Advantages

• Most implementations make it trivial to find feature importance
• It is very easy to Tune
• Random Forests excel with highly non-linear relationships in the data.

Main Disadvantages

Can perform worse than Gradient Boost

Gradient Boosted Machines tend to perform better under both of the following conditions:

1. We correctly tune the relatively complicated hyperparamters of GBM.
2. Either 1) your data fits in ram (for sklearn) or 2) your problem is not a multiclass classification problem (for Spark).
3. (My understanding, not certain) Non-linear relationships

Slow to Predict

Since predicting a new observation requires running the observation through every tree, Random Forests will often perform too poorly for real-time prediction.

Doesn’t behave well for very sparse feature sets

In this case, SVM and Naive Bayes tend to perform better than Random Forests. One of the reasons for this is because each tree only has access to $\sqrt{n}$ features by default. If very few features are of any importance, most trees will miss important features.

Using it in sklearn

Below is an example of using a Random Forest with 50 trees:

model_rf = RandomForestClassifier(n_estimators=200, oob_score=True, verbose=1,
                                  random_state=2143, min_samples_split=50, 
                                 n_jobs=-1)
fitted_model = model_rf.fit(X, y)

The oob_score argument tells the classifier to return our out of sample (bag) error estimates. The min_samples_split=50 argument tells the classifer to only create another branch of the tree if the current branch has more than 50 observations. n_jobs=-1 tells SKlearn to use all the cores on my machine.

Using it in Spark

An example of using Random Forests in Spark can be found here. Here is the same example as in SKlearn:

Practical tips

• A good way to prevent overfitting is to set a relatively high tree-splitting threshhold. This is the min_samples_split argument in SKLearn.
• We can easily check if we are overfitting by looking at the out of bag error.
• More trees are always better than fewer. The returns start to dominish quickly.
  • Source here
• Having trees that are too deep can lead to overfitting. This can be avoided by increasing the number of trees.
• The default number of features ($\sqrt{n}$) is usually a sufficiently good value.
• After picking the best Random Forest with your out of bag errors,

References

1. Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. The elements of statistical learning. Vol. 1. Springer, Berlin: Springer series in statistics, 2001. APA
2. http://www.slideshare.net/0xdata/jan-vitek-distributedrandomforest522013
3. http://scikit-learn.org/stable/modules/ensemble.html
4. Random Forests by Leo Breiman

Footnotes